Tein pääsykoekirjan harjoitustehtävät, joissa mitta-asteikot piti nimetä ja mä osasin ne KAIKKI oikein! Oon todella ylpeä itsestäni, koska oikeasti muistin ensinäkin kaikki asteikot, toisenakin muistin myös mitkä oli laadullisia, määrällisiä ja mitkä olivat niiden kriteerit. Yhden tehtävän kanssa olin tosin eri mieltä kirjan kanssa: tehtävässä kysyttiin pankkitilin saldon mitta-asteikkoa. Oikea vastaus oli suhdeasteikko, mutta olen eri mieltä, koska tilin saldo voi olla myös miinuksella, jolloin sillä ei ole absoluuttista 0 -pistettä.. Kirjan kirjoittavat ovat kuitenkin kanssani eri mieltä.
Noh, joka tapauksessa on aika siirtyä kertaamaan luku 3, joka on mielestäni kaikkein simppelin ja mieluisin aihealue (pahoittelut tökeröistä töherryksistä joiden tarkoitus on esittää kuvaajia — en uskaltanut ottaa kuvia suoraan kirjasta, kun en ollut varma tekijäsuojauksista, joten tyydyin ottamaan kuvat omista muistiinpanoistani):
Tutkimusaineiston valmistelu ja graafinen kuvaileminen
Kuvailevassa tilastotieteessä tutkimuksen kohteena olevia ilmiöitä esitetään usein tiivistetysti taulukoina ja graafisina kuvioina, koska sanallinen kuvaileminen on usein hankalaa. Taulukoiden ja kuvioiden tarkoitus on tiivistää ja havainnollistaa aineisto. Kuvaajien avulla voidaan saada muodostettua alustava käsitys aineiston sisältämistä ilmiöistä ennen varsinaiseen tilastolliseen päätöksentekoon siirtymistä. Kuvion tulee olla niin selkeä, että se on ymmärrettävissä ilman muuta tekstiä.
Tavoitteena on esittää tutkimuksen tulokset mahdollisimman selkeästi, havainnollisesti ja totuudenmukaisesti. Kuvaajan valinnassa on mahdollista vaikuttaa siihen, mitä aineiston ominaisuuksia korostetaan. Totuudenmukaisinta on, että tulos näkyy kuvaajasta vaivattomasti.
Akselin alku- ja loppupisteen valinnalla on sinällään vääristetä tutkimuksen tuloksia, mutta valinta vaikuttaa siihen, mitä tietoja kuvaaja korostaa. Turhan pieniä tietomääriä ei kannata esittää kuvaajassa. Tulee muistaa, että monessa tapauksessa tarkkojen lukuarvojen esittäminen on tehokkaampi tapa viestiä.
- Havaintomatriisi ja taulukointi
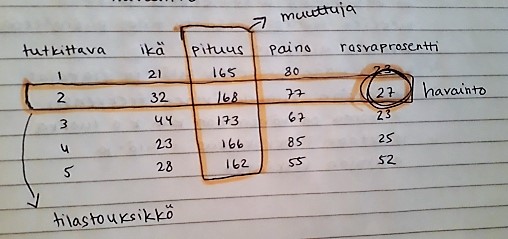
Tilastoaineiston käsittely aloitetaan muodostamalla kerätystä tilastotiedosta aluksi havaintomatriisi, joka toimii analyysin lähtökohtana. Tilastollisen analyysin tavoitteena on yleensä paljastaa havaintomatriisin sisältämät ilmiöt ja kuvailla ne helposti ymmärrettävällä tavalla.
Vaakarivi sisältää aina yhteen tilastoyksikköön liittyvät muuttujien arvot ja jokainen pystyrivi sisältää yhden muuttujan kaikki arvot. Vaaka- ja pystyrivin leikkauspisteessä on siten aina yksittäinen havainto.
Tilastoaineisto voidaan myös luokitella, eli yksinkertaisesti taulukoida aineistossa olevia kategorisia muuttjia laskemalla lukumäärät aineistoissa (frevenssit). Jatkuville muuttujille frekvenssien laskelminen ei ole mielekästä, jolloin voidaan muuttujat ensin luokitella. Luokkien olisi syytä olla tasavälisiä. Ei ole mitään yksiselittistä sääntöä siitä, kuinka monta luokkaa tulisi muodostaa. Sopiva luokkinen määrä on 6-10, mutta määrään vaikuttaa muun muassa tilastoaineiston laajuus ja maksimi ja minimiarvot. Luokkinen peitto (leveys) lasketaan:
suurin havainto/pienin havainto
Avoimia luokkia tulisi välttää ja luokkaväliksi ja luokkien alarajoiksi kannattaa valita sopivan pyöreitä lukuja.
Frekvenssijaukauman laskemisen lisäksi aineistosta voidaan laskea myös kahden kategorisen muuttujan välistä yhteisjakaumia, jolloin lopputuloksena on kaksiuloitteinen frekvenssijakauma (eli ristiintaulukointi) ja lopputuloksena saatavasta taulukosta käyetään nimeä kontigenssitaulu. Esimrkiksi koulutuksen jakautuminen sukupuolittain. Tällä tavalla voidaan arvioida, onko sukupuolella yhteys koulutukseen ja se voi paljastaa sukupuolten väliset erot.
Kuvataan yleensä epäjakuvan muuttujan arvojen frekvenssijakaumaa. Jokaisnen muuttujan luokka kuvataan omana pylväänään ja sillä voidaan esittää muuttujan frekvenssijakauma, eli kuinka monta havaintoa kuhunkin muuttujan luokkaan sisältyy. Vaikka tälläset kuvaajat ovat selkeitä, ne eivät ole tilankäytön kannalta tehokkaita, sillä kuvaaja vie paljon tilaa. Pylväskuvaajan avulla voidaan esittää myös yhteisjakauma.
Yhteisjakauma voidaan esittää myös niin, että pylväät esitetään pinottuina sen sijaan, että ne piirrettäisiin vieretysti. Etuna on, että pylväiden kokonaiskorkeus kertoo suoraan toisen muuttujan jakauman koko aineistoissa. Käytännössä on kuitenkin parempi piirtää pylväät vieretysti., jolloin korkeutta on helpompi verrata.
Jos aineistossa on mtattu samaa suuretta useammalla eri tavalla, tälläsiset muuttujat voidaan kuvata samassa pylväsdiagrammissa. Muuttujat voidaan esittää samaa y- akselia hyväksi käyttäen. Tällöin aineisto hahmottuu yhdellä silmäyksellä.

Pylväskuvioilla voidaan esittää myös arvoja, joista osa on positiivisia ja osa negatiivisia. Tällöin pylväät piirretään yksinkertaisesti joko x -akselin yläpuolelle tai alapuolelle sen mukaan, kuvaako ne positiivisia vai negatiivisia arvoja. Tällä tavalla on helppo vertailla kuvaajassa esitettyjen lukujen etumerkkejä.
Pylväskuvio voidaan esittää myös niin, että pylväät ovat vaakasuorassa. Tälläsestä kuvaajasta käytetään nimitystä palkkikuvio. Sen etuna on, että kuvailtavien luokkien nimet ovat helpommin luettavissa, kun palkkeja on enemmän. Pylvään kuvioon voidaan myös lisätä tarkkoja arvoja.

Muistuttaa ulkonäöltään pylväsdiagrammia, mutta sitä käytetään kuitenkin jatkuvien muuttujien jakauman kuvaamiseen. Histogrammia piirtäessä jatkuvat muuttujat tulee ensin luokitella sopivan suuruisiin luokkiin. Jokainen luokka kuvataan pylväällä. Pylvään korkeus kuvaa aina havaintojen lukumäärää. Histogrammin pylväät piirretään aina yhteen erotukseksi pylväskuvaajasta. Samalla sillä korostetaan sitä, että kuvaaja esittää jatkuvaa muuttujaa.
Käytetään ennen kaikkea ajan mukana muuttuvien suureiden, eli aikasarjojen, graafiseen esittämiseen. Tarkoitus on antaa yleiskuva tutkittavan suureen suunnasta ja muutosnopeudesta eri aikoina. Mitä jyrkemmässä kulmassa viiva on tiettynä ajankohtana, sitä nopeamapaa muutos on tuolloin ollut. Viivadiagrammia käyttäessa tulee kiinnittää erityisesti huomiota y -akselin valintaan. Liian pieni (suppea) skaala korostaa muutosnopeutta, jolloin pienetkin muutokset näkyvät suurina hyppäyksinä, vastaavasti liian suuri (laaja) skaala peittää pienet muutokset.

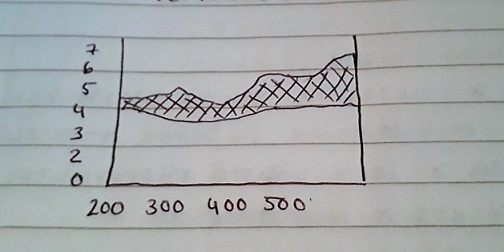
Aluekuvio on eräänlainen viivakuvaajan erikoistapaus. Aluekuviossa koko viivan tai viivvojen alle jäävä alue väritetään tai rasteroidaan. Aluekuvio ei välttämättä ole hyvä valinta, koska se voidaan tulkita väärin eikä vertaileminen ole helppoa. Hyvä vaihetoehto esimerkiksi kuvaamaan menojen ja rahoituksen kehitystä.
Käytetään kategoristen muuttujien kuvaamiseen silloin, kun halutaan havainnollistaa kokonaisuuden jakautumista osiin. Jokaisen luokan kokoa edustaa sekrotin pinta-ala, joka on suoraan verrannollinen luokan kokoon. Usein luokkakohtaiset frekvenssit tai prosenttiosuudet merkitään suoraan kuvaajaan. Sektorikuvaaja on intuitiivinen ja kuitenkin monella tapaa ongelmallinen. Se vie paljon tilaa, tarkka keskinäinen vertaileminen on hankalaa ja usein on pakko merkitä luokkakohtaiset prosenttiosuudet. Tätä kuvaajaa kannattaa yleisesti välttää. Etuna kuitenkin on, että siinä voidaan kuvata samanaikaisesti useamman muuttujan frekvenssijakauma, jolloin kuvaajan pinta-ala voidaan käyttää tehokkaammin hyödyksi.
Sirontakuvion avulla havannollistetaan kahden muuttujan (x ja y) välistä riippuvuutta. Yksi piste esittää aina yhtä tilastoyksikköä, niin, että pisteen sijainti x -akselilla kuvaa tilastoyksikön saamaa arvoa x -muuttujalla ja vastaavasti sijainti y -akselilla sen arvoa y -muuttujalla. Tällä tavalla voidaan arvioida onko muuttujien x ja y välillä mahdollisesti jonkinlaista riippuvuutta, eli muuttuvatko y -muuttujen arvot systemaattisesti x -muuttujan arvojen kasvaessa tai pienentyessä.